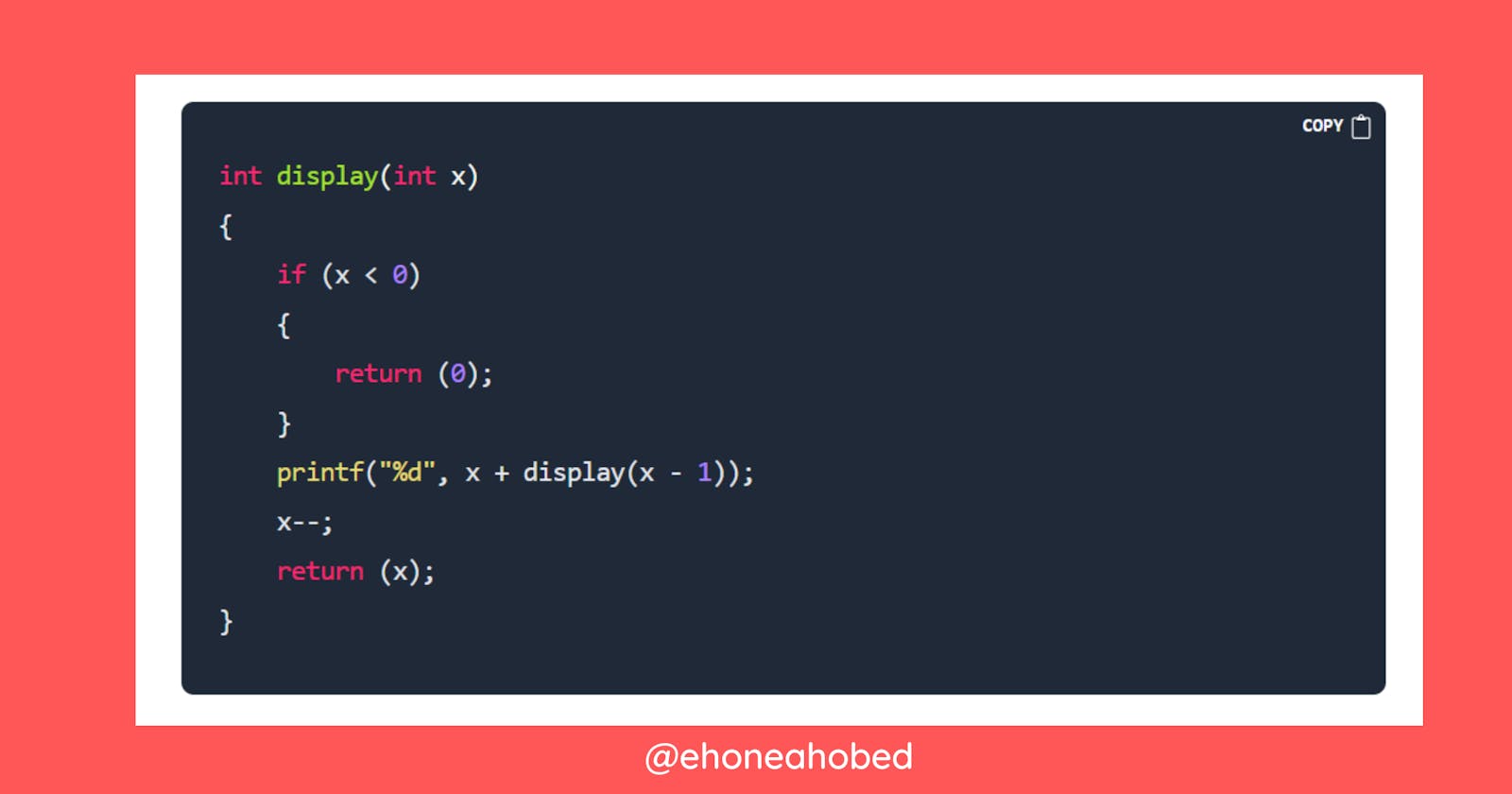
What will this Recursive function in C Print and what is the logic behind it?

A practical recursion problem with its logic helping you understand how recursion works.

PublishedJune 23, 2022

What will this Recursive function in C Print and what is the logic behind it?

Heya! 👋 I love helping people, and one of the best ways I do this is by sharing my knowledge and experiences. My journey reflects the power of growth and transformation, and I’m here to document and share it with you.

I started as a pharmacist, practicing at a tertiary hospital in the Northern Region of Ghana. There, I saw firsthand the challenges in healthcare delivery and became fascinated by how technology could offer solutions. This sparked my interest in digital health, a field I believe holds the key to revolutionizing healthcare.

Determined to contribute, I taught myself programming, mastering tools like HTML, CSS, JavaScript, React, PHP, and more. But I craved deeper knowledge and practical experience. That’s when I joined the ALX Software Engineering program, which became a turning point. Spending over 70 hours a week learning, coding, and collaborating, I transitioned fully into tech.

Today, I am a Software Engineer and Digital Health Solutions Architect, building and contributing to innovative digital health solutions. I combine my healthcare expertise with technical skills to create impactful tools that solve real-world problems in health delivery.

Imposter syndrome has been part of my journey, but I’ve learned to embrace it as a sign of growth. Livestreaming my learning process, receiving feedback, and building in public have been crucial in overcoming self-doubt. Each experience has strengthened my belief in showing up, staying consistent, and growing through challenges.

Through this platform, I document my lessons, challenges, and successes to inspire and guide others—whether you’re transitioning careers, exploring digital health, or diving into software development.

I believe in accountability and the value of shared growth. Your feedback keeps me grounded and motivated to continue this journey. Let’s connect, learn, and grow together! 🚀

Comments

Join the discussion

No comments yet. Be the first to comment.

C Programming

Part 12 of 40

From today, I will be starting lessons on C programming in my ALX Software Engineering class and I look forward to sharing with you everything I learn through this series.

Up next

Monty Bytecode Interpreter using C

In order to practicalize our knowledge of data structures like stacks and queues in C language, we were tasked with building a C program that acts as a Monty bytecode interpreter. What is the Monty Bytecode Interpreter This is a C program that will ...

More from this blog

Choosing the Right AI Model for the Job

Imagine you have access to several AI models. One is extremely powerful but expensive. Another is fast and cheap but less capable. A third is excellent at coding but weaker at reasoning. Which on

Jun 16, 202610 min read

How Source Documents Make AI More Reliable

In the last lesson, you learned something important: AI can generate information that sounds convincing while still being completely wrong. That happens because AI primarily predicts patterns in langu

Jun 2, 20268 min read

Why AI Sounds Smart Even When It Is Wrong

One of the strangest things about modern AI is this: It can sound extremely intelligent while still being completely wrong. That is what makes AI both impressive and dangerous at the same time. You

Jun 2, 20269 min read

Prompt Engineering: Thinking Like a Professional AI User

At this point, you already understand something many AI users never fully realize: AI does not read prompts like humans do. It processes: tokens patterns structure and attention distribution Tha

May 30, 20268 min read

How AI actually processes your prompt under the hood

One of the biggest mistakes people make when using AI is assuming the AI reads like a human. It does not. Humans: infer meaning read between the lines fill in missing context guess intentions AI

May 30, 20268 min read

Dr. Ehoneah Obed

86 posts

Software engineer writing about systems: in code, in learning, in life. I reverse-engineer complex problems into frameworks. Pharmacist → SWE → Founder.

#include <stdio.h>

int display(int x)
{
    if (x < 0) 
    {
        return (0);
    }
    printf("%d", x + display(x - 1));
    x--;
    return (x);
}

int main(void)
{
    display(4);
    return (0);
}

To be able to find what the above program will print, you need to understand recursion and how recursive functions work.

The simplest way will be to run the code in a compiler, but being able to deduce it based on the logic of the program is what the question seeks.

I am going to go on and explain the logic behind the code, presuming that you know about recursion and recursive functions. If you have no idea about them, then try and read on them before.

Since the question is looking for the output, we have to be interested in any line of code that prints out something to the screen.

In the code above, you can see that there is only one line that prints out something to the screen and that line is:

printf("%d", x + display(x - 1));

However, the print line even though within the display() function also calls another display() function which makes the function a recursive function.

The presence of the recursion of the function also draws our attention to the return value for the function. This is because, the return value is what will be provided anywhere the function is called.

This means that we need to figure out both what is printed out and what is returned in order to get the right output for the whole code.

Let's therefore take them one by one.

What does this function do and what does it return

int display(int x)
{
    if (x < 0) 
    {
        return (0);
    }
    printf("%d", x + display(x - 1));
    x--;
    return (x);
}

The first line of the body of the function checks to see if the variable (x) passed to it is less than zero and returns zero if that is true.

The function then goes on to print the sum of the variable plus the return value of the display() function when the argument for the function is x-1.

In the next line, there is a decrement on the variable x before returning the current value of x. The decrement on x means that, we will subtract one from x and return the resulting value.

This means that every time, the display() function is called, it returns one less than the number that was passed to it as an argument. An example will be if we call display(2), then it is going to return 2-1 which be 1.

Since the question gave display(4), it means we need to have the return values for 4, then the printf statement in there will also require the return value for 3 which in turn will require return values for 2, etc.

We will have to keep reducing the numbers till we get to zero. So, let's have a table with the numbers and their return values:


Display function argument	Return value
4	3
3	2
2	1
1	0
0	-1
-1	0

Now that we know what the function does and the values it returns at each stage, we can go ahead look at what the function prints at each stage.

What does the function print at each stage?

printf("%d", x + display(x - 1));

At each stage, the function prints the sum of the argument (x) passed to the function and the return value of the display() function with argument of one less than the initial argument (x-1).

Since we know that, the function in the question above runs multiple times with values starting from 4 down to 0, we have to find the value that will be printed with each value.

Let's use a table to illustrate that.


Display function argument	What to print value	Argument + Return value	Value printed
4	4 + return value for display(3)	4 + 2	6
3	3 + return value for display(2)	3 + 1	4
2	2 + return value for display(1)	2 + 0	2
1	1 + return value for display(0)	1 + -1	0
0	0 + return value for (-1)	0 + 0	0

Because of the recursion, the code will print that of display(0) first followed by display(1) then continuously till the last one (display(4) in this case) is printed.

As such, you have the final output being:

Conclusion

I hope I was able to simplify this enough but if you have questions on any of the things I explained above or have some suggestions, you can comment it down below or hit me up on Twitter via a DM and let's chat it out.

Thanks for reading.

Command Palette